A time series analysis on precipitation in Phyang
visualisation
humanitarian
R
A time serie analysis of precipitation in Ladakh
Exploratory analysis
Data was obtained using Google Earth Engine and taken from the dataset CHIRPS Pentad. For reference on R command and tools to be used a great source is the online book on forecasting by Rob J Hyndman and George Athanasopoulos.
Plot of monthly precipitation from 1981 to 2021 in Phyang and histogram of all monthly rainfall.
Rolling average, sum, median
Plot shows the rolling average, max, median and sum over a period of 36 months. A reduction in precipitation can be observed between 1998-2010.
Sub-annual series
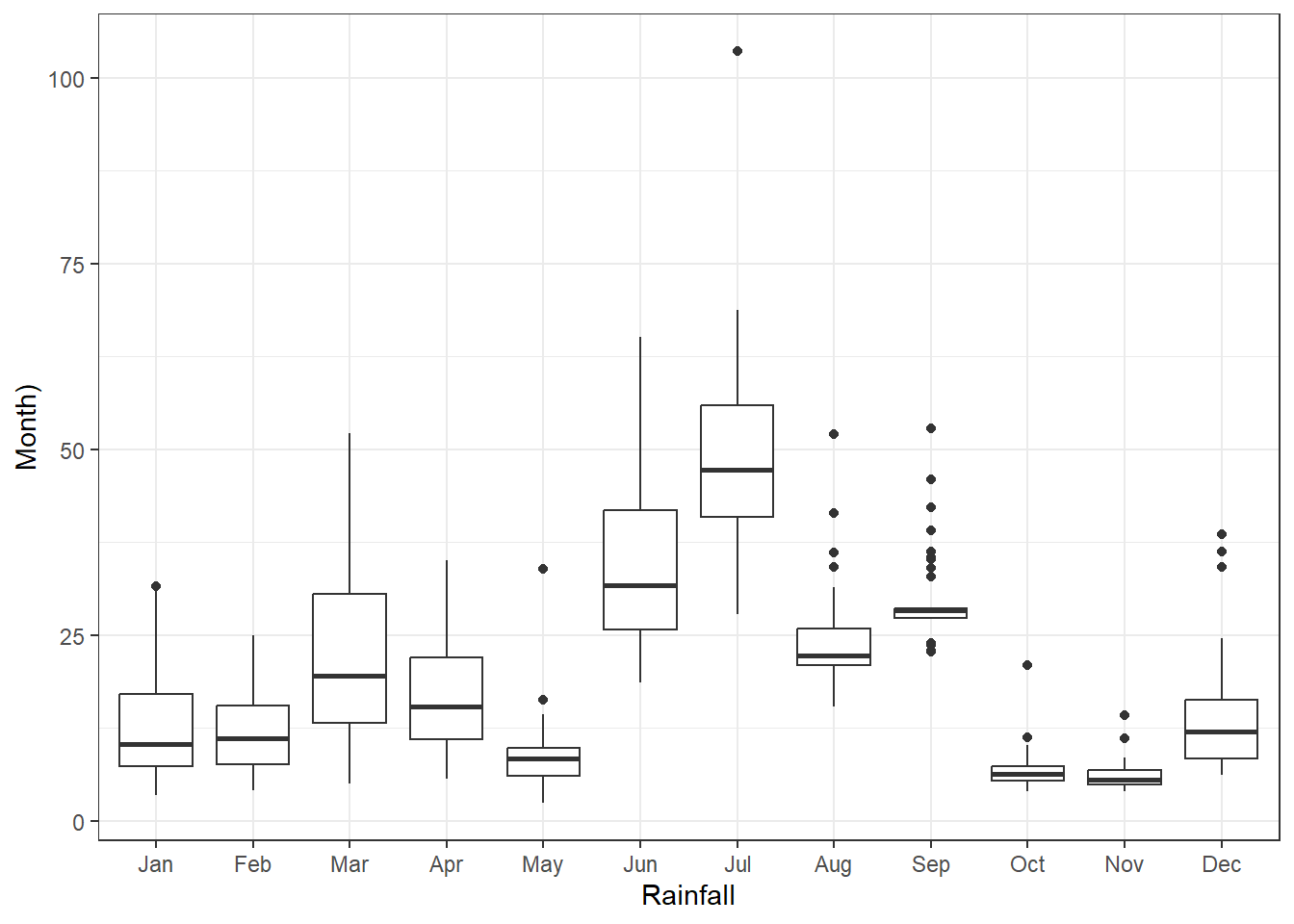
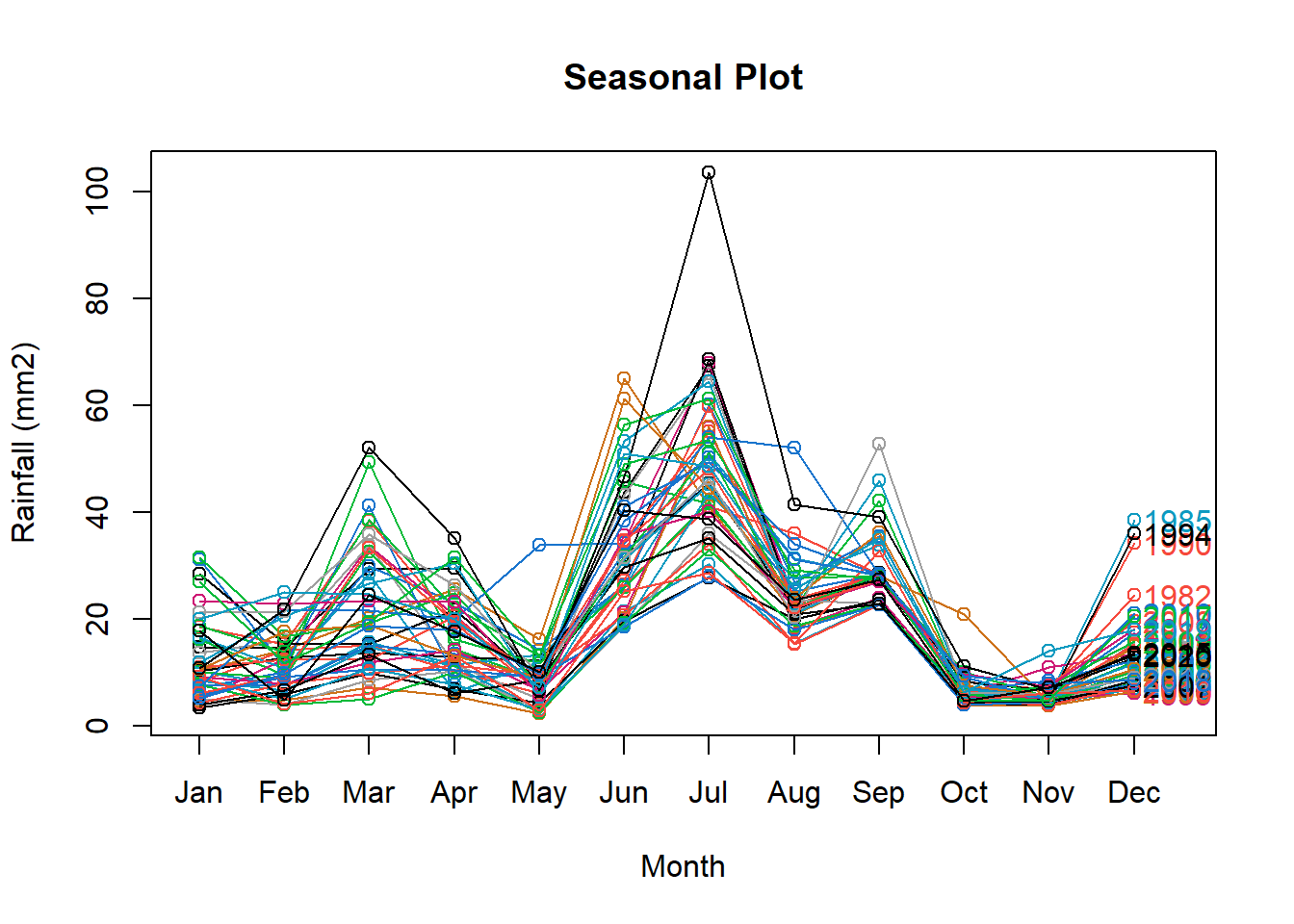
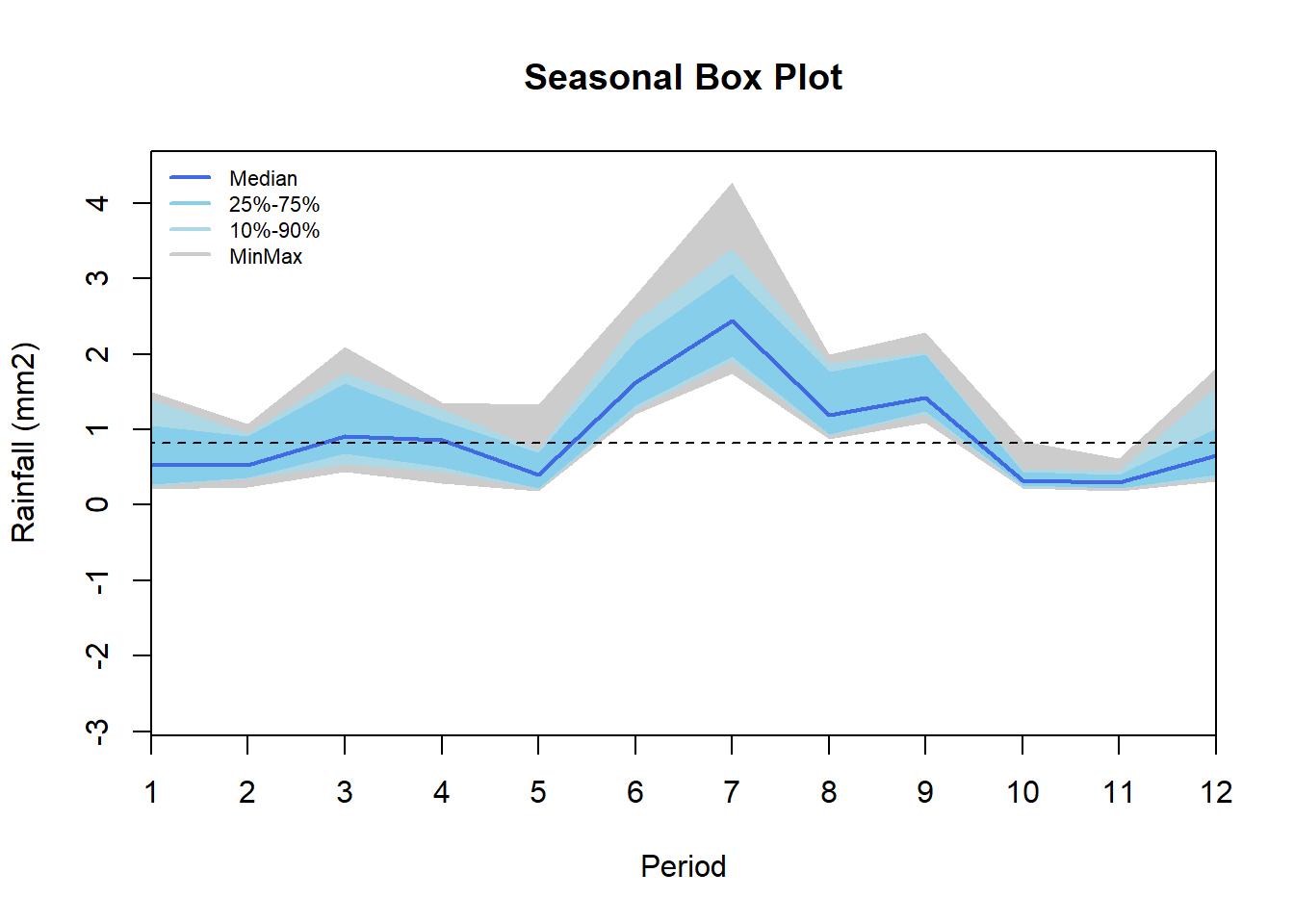
Rainfall data disaggregated per month showing highest rain in June and July and lowest in May October and November. Highest variability across years in found in March, June, July while lowest in September, October and November. Additionally distribution for the month of March(black line), June (green), and July (red) is shown.
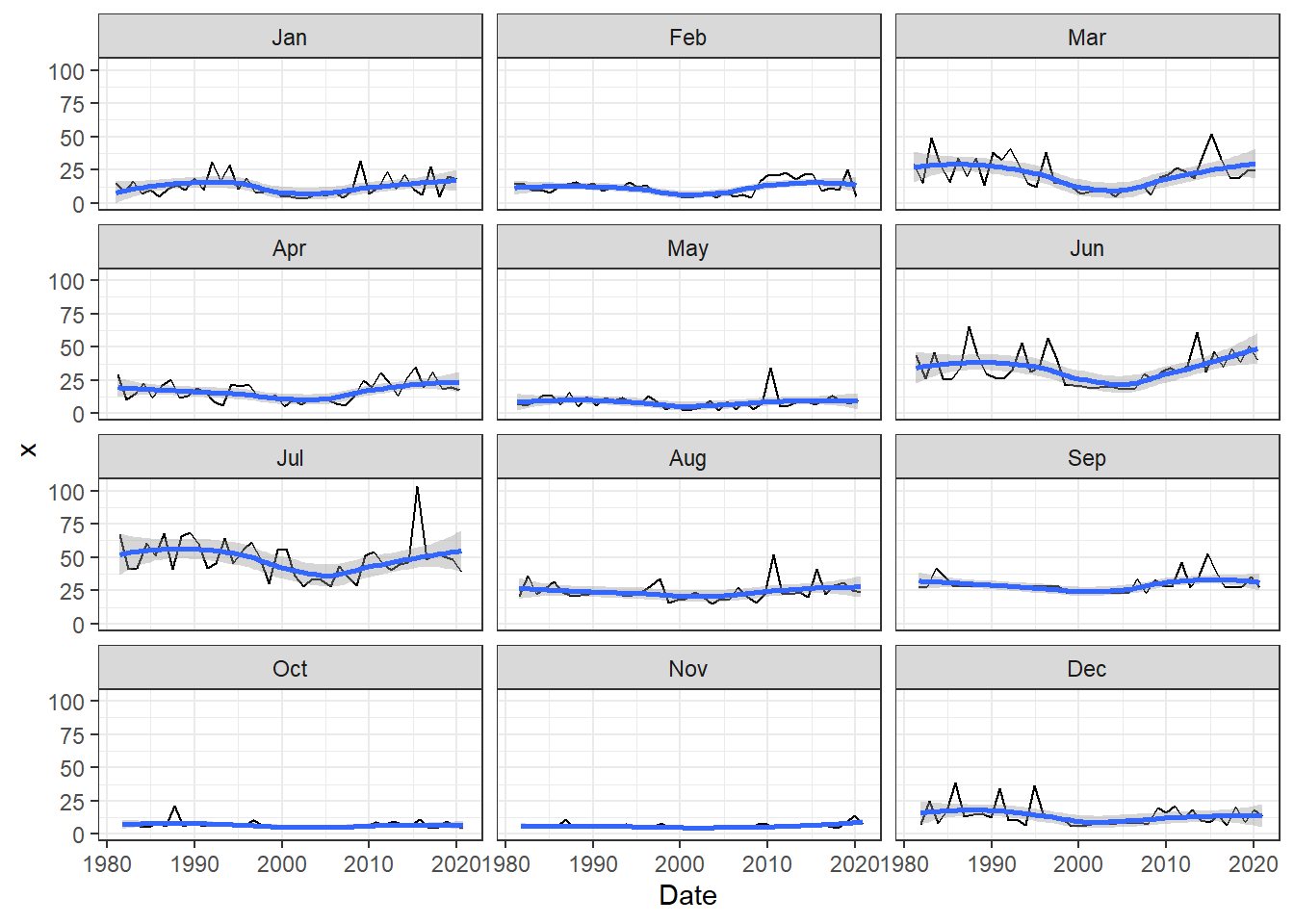
Decomposition
The strength of the trend and seasonal measured between 0 and 1, while “1” means there’s very strong of trend and seasonal occurred.
Trend.Strength Seasonal.Strength
1 0.4 0.8Seasonality analisys
Results of statistical testing
Presence of trend not tested.
Evidence of seasonality: TRUE (pval: 0)
Results of statistical testing
Presence of trend not tested.
Evidence of seasonality: TRUE (pval: 0)
Results of statistical testing
Presence of trend not tested.
Evidence of seasonality: TRUE (pval: 0)
Forecasting
Train period from 1981 to 12.2015 and test period from 01.2016
Data it is checked against stationary state.
#######################
# KPSS Unit Root Test #
#######################
Test is of type: mu with 5 lags.
Value of test-statistic is: 0.3834
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.347 0.463 0.574 0.739
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression none
Call:
lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-31.409 -4.913 2.164 10.967 73.397
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z.lag.1 -0.19147 0.03094 -6.188 1.32e-09 ***
z.diff.lag -0.19143 0.04498 -4.256 2.51e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 15.7 on 476 degrees of freedom
Multiple R-squared: 0.1507, Adjusted R-squared: 0.1471
F-statistic: 42.23 on 2 and 476 DF, p-value: < 2.2e-16
Value of test-statistic is: -6.1878
Critical values for test statistics:
1pct 5pct 10pct
tau1 -2.58 -1.95 -1.62Using 95% as confidence level, the null hypothesis (ho) for both of test defined as:
KPSS Test: Data are stationary at 10% confidence (value of 0.3834). DF Test:
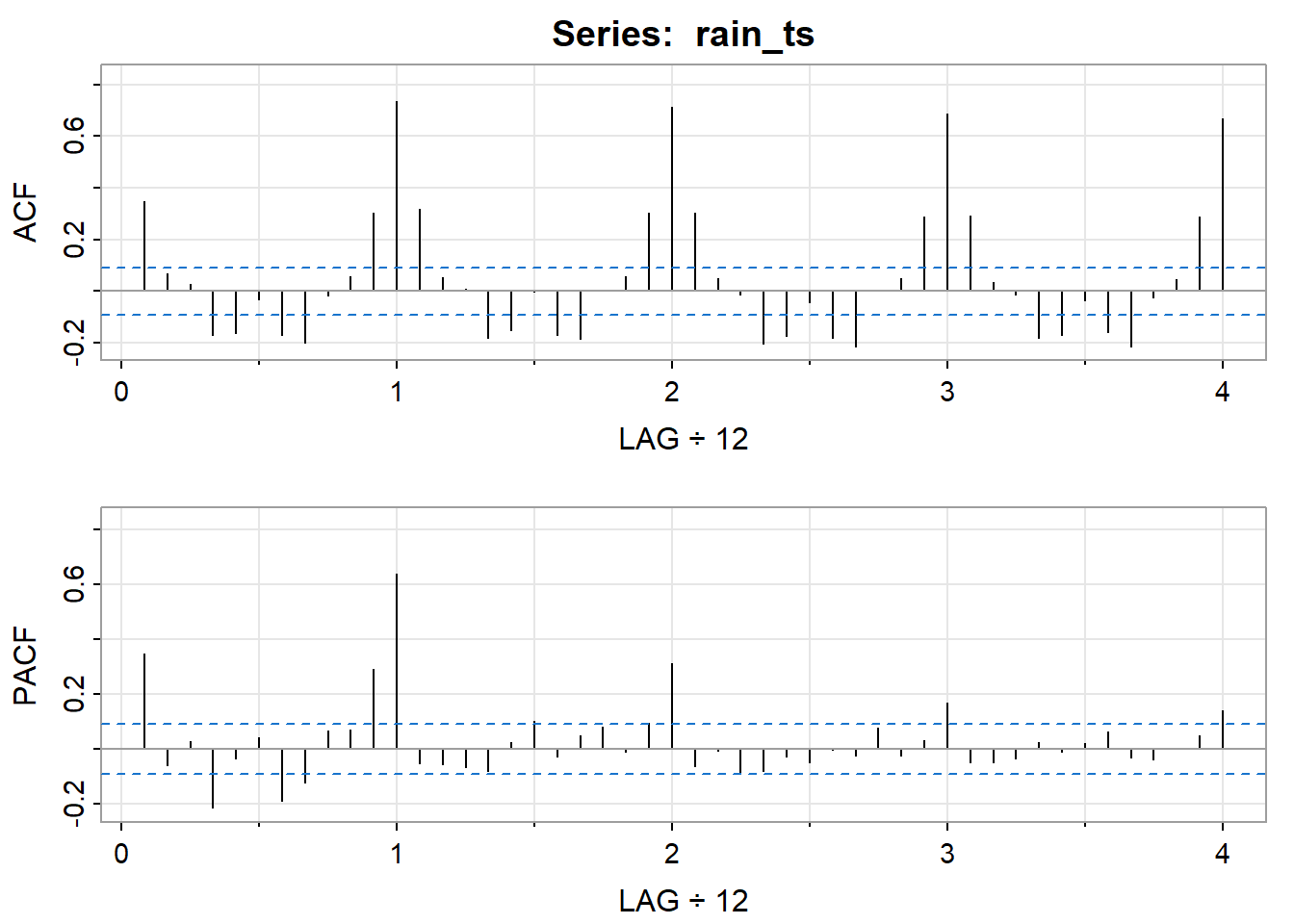
ARIMA analysis
Using different models for ARIMA.
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
ACF 0.35 0.07 0.03 -0.17 -0.16 -0.03 -0.17 -0.20 -0.02 0.06 0.30 0.74
PACF 0.35 -0.06 0.03 -0.21 -0.04 0.04 -0.19 -0.12 0.06 0.07 0.29 0.64
[,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
ACF 0.32 0.05 0.01 -0.18 -0.15 0.0 -0.17 -0.19 0.01 0.06 0.3 0.71
PACF -0.05 -0.06 -0.07 -0.08 0.02 0.1 -0.03 0.05 0.08 -0.01 0.1 0.31
[,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36]
ACF 0.30 0.05 -0.01 -0.20 -0.17 -0.04 -0.18 -0.21 0.01 0.05 0.29 0.69
PACF -0.07 -0.01 -0.09 -0.08 -0.03 -0.05 0.00 -0.03 0.08 -0.03 0.03 0.17
[,37] [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
ACF 0.29 0.03 -0.01 -0.18 -0.17 -0.04 -0.16 -0.21 -0.03 0.05 0.29 0.67
PACF -0.05 -0.05 -0.03 0.02 -0.01 0.02 0.06 -0.03 -0.04 0.00 0.05 0.14
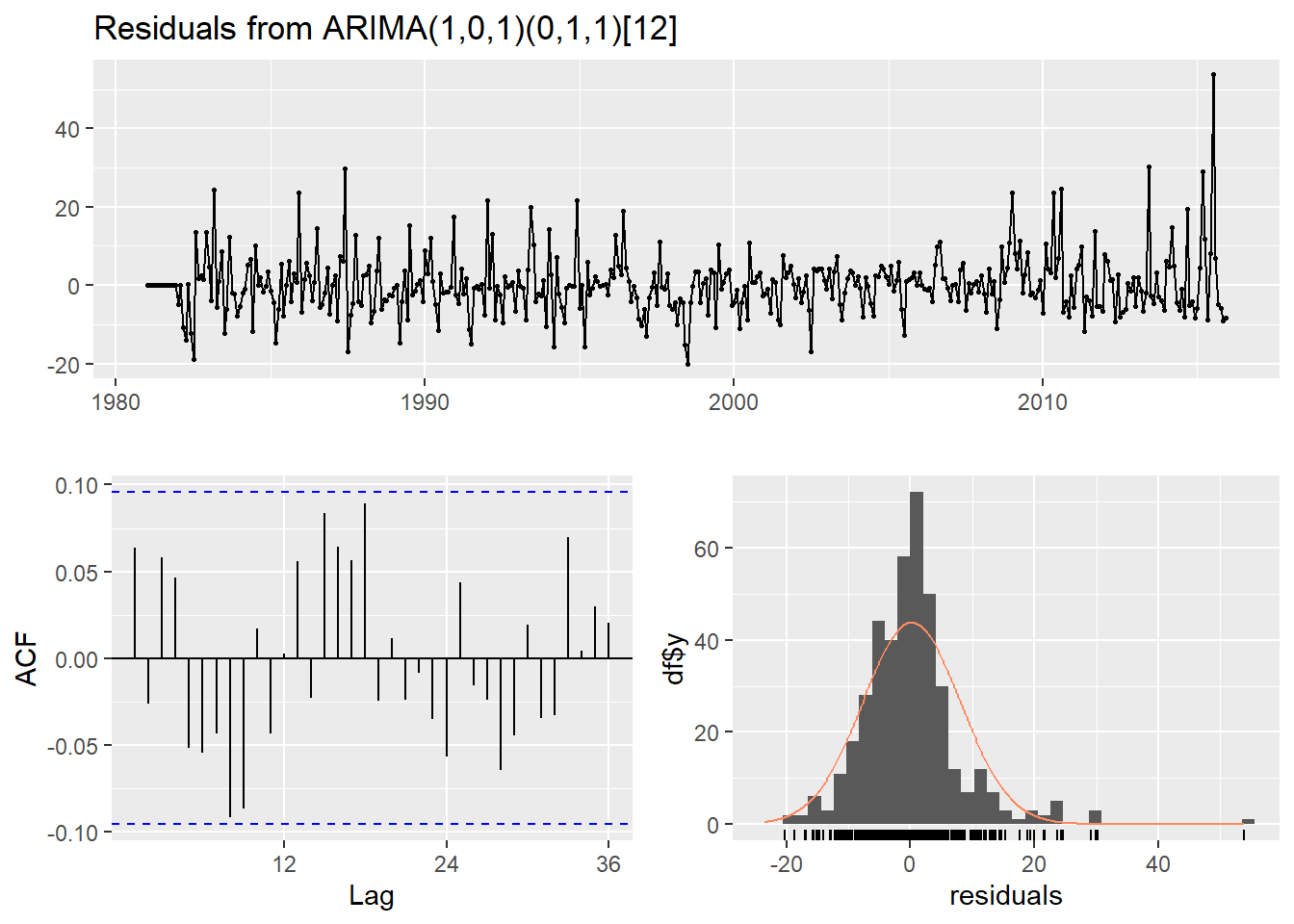
Ljung-Box test
data: Residuals from ARIMA(1,0,1)(0,1,1)[12]
Q* = 29.36, df = 21, p-value = 0.1056
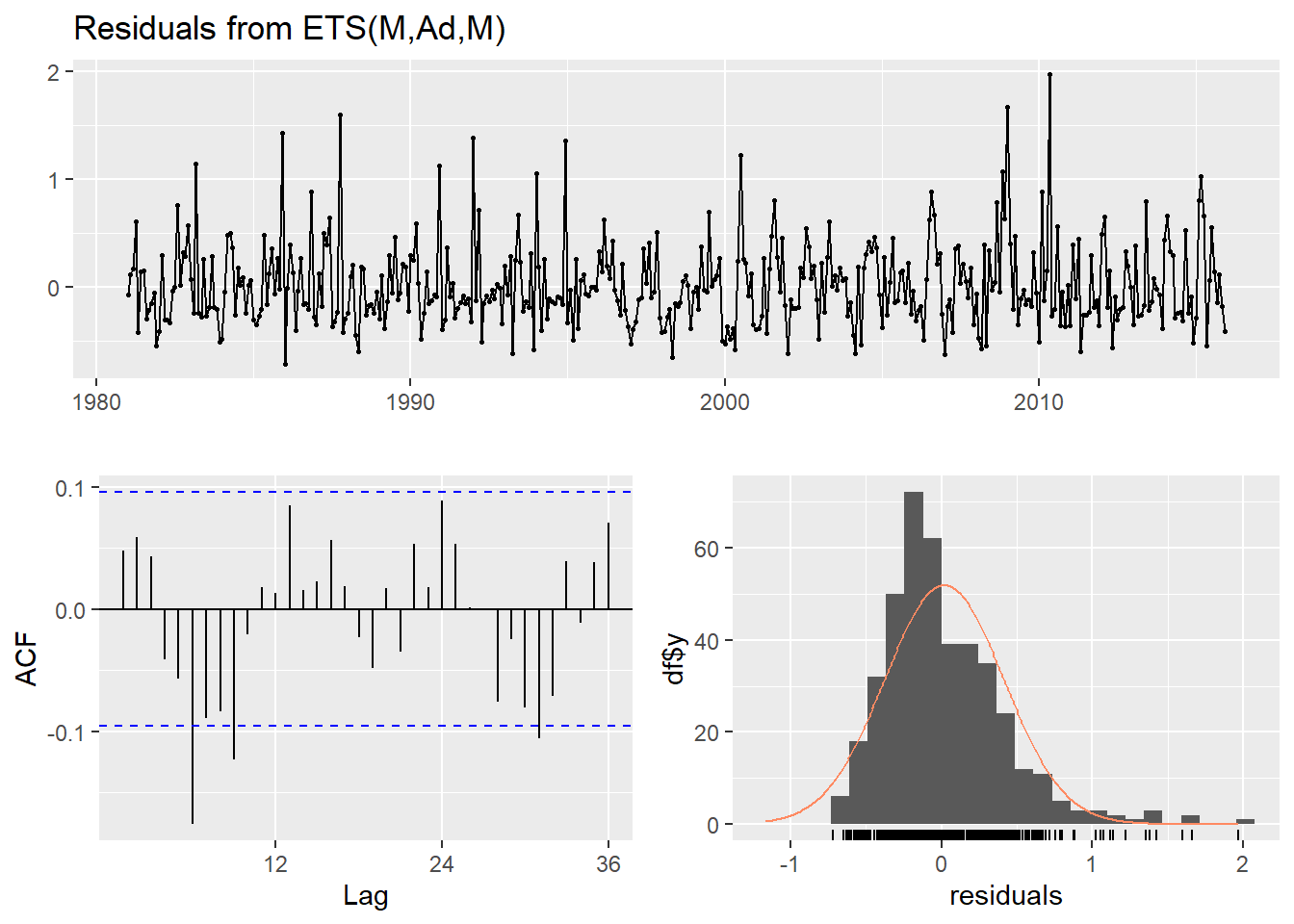
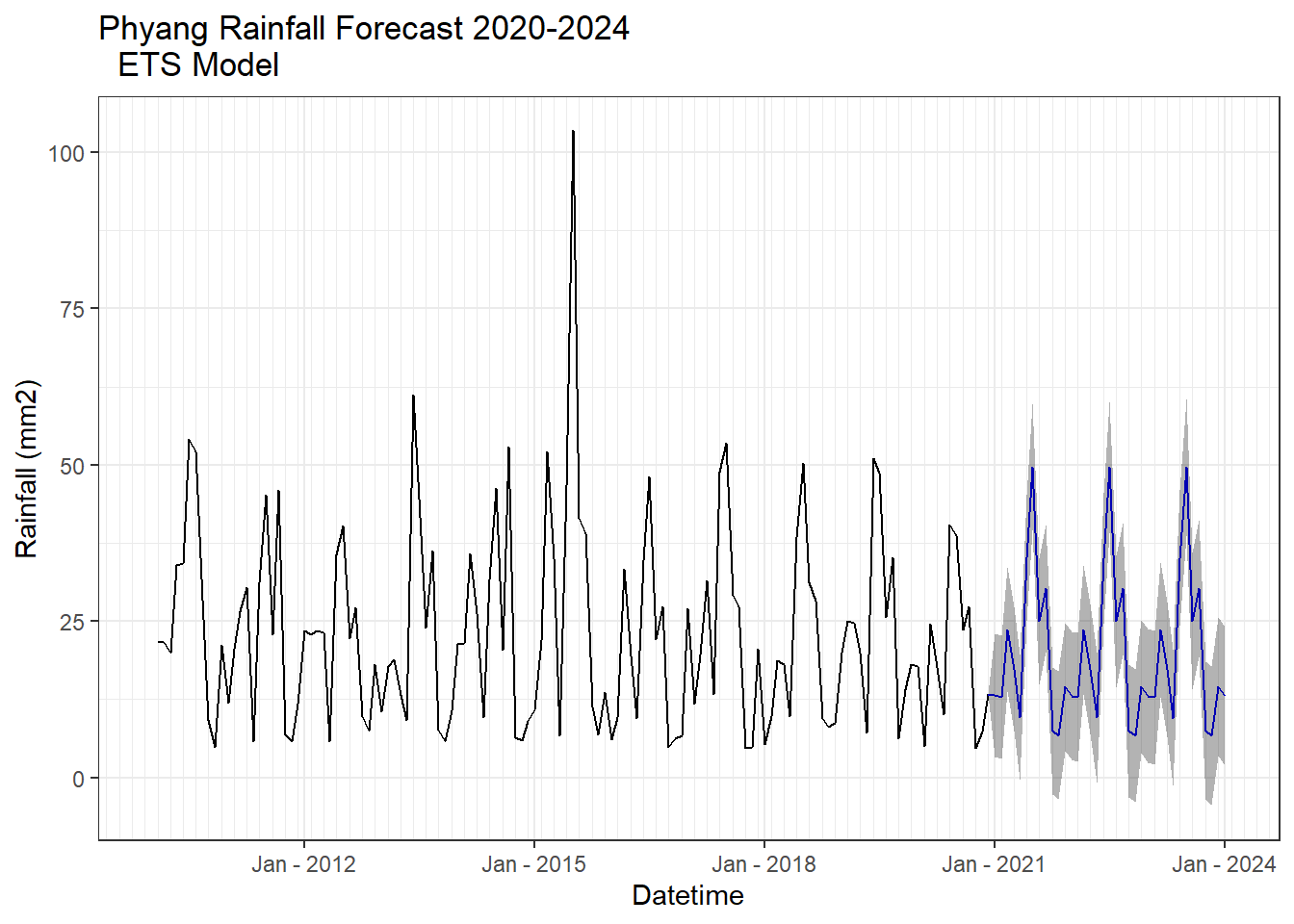
Model df: 3. Total lags used: 24ETS model
Ljung-Box test
data: Residuals from ETS(M,Ad,M)
Q* = 43.792, df = 24, p-value = 0.008067
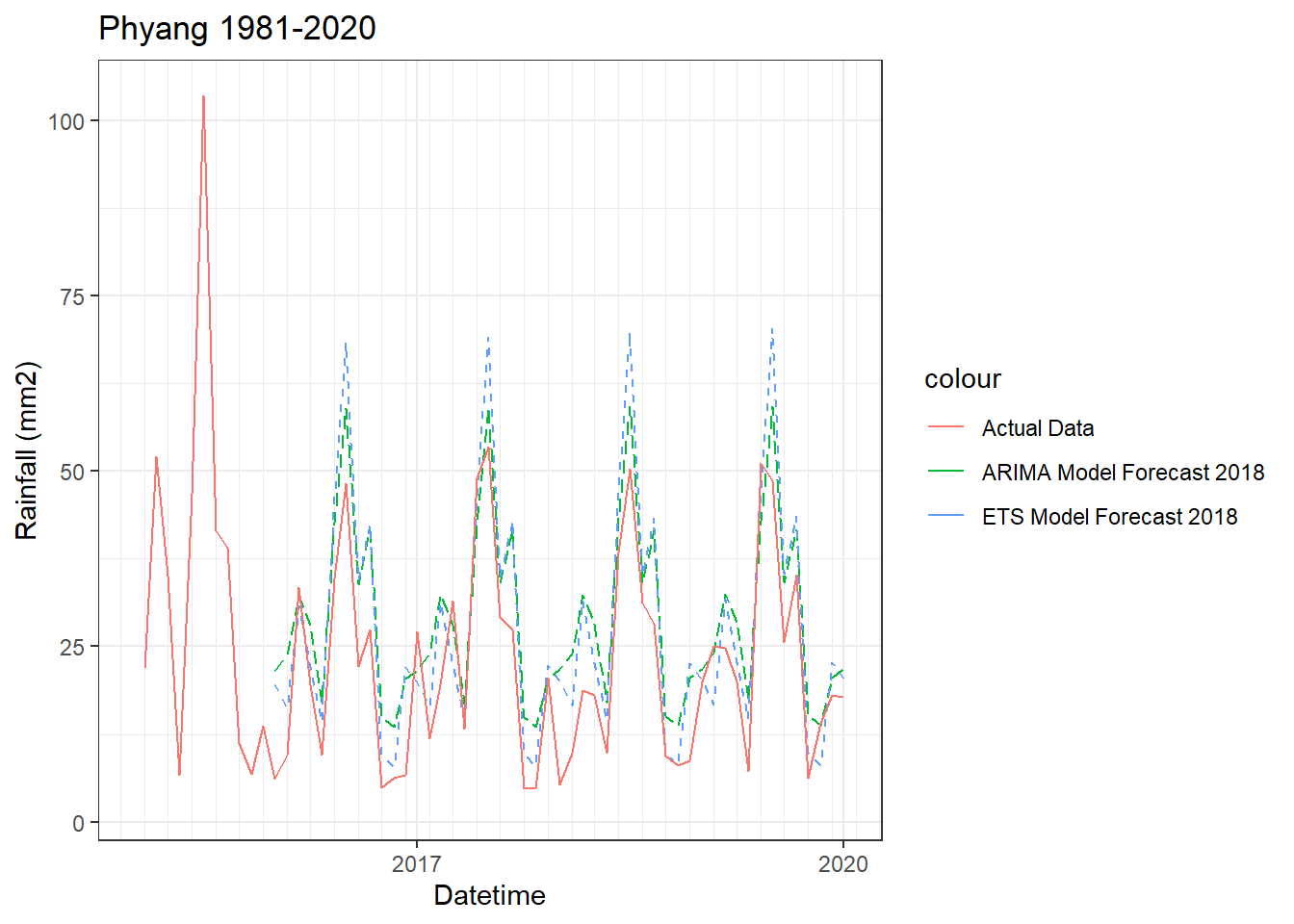
Model df: 0. Total lags used: 24Forecasting
Accuracy of models
ME RMSE MAE MPE MAPE MASE
Training set 0.170763 7.87356 5.388082 -9.139575 35.28552 0.8073011
Test set -9.964325 10.87446 10.165830 -99.206968 99.81011 1.5231554
ACF1 Theil's U
Training set 0.063420750 NA
Test set -0.004907483 0.9583204 ME RMSE MAE MPE MAPE MASE ACF1
Training set 0.285966 7.61933 5.34607 -13.12624 33.12538 0.8010065 0.02948987
Test set -8.700370 10.85699 9.13186 -73.04490 74.33643 1.3682347 0.27990111
Theil's U
Training set NA
Test set 0.7923204##Forecasting and plot
